What is Insertion Sort?
Insertion Sort is a simple, intuitive sorting algorithm that builds the final sorted array one element at a time.
It works similar to how you might sort a hand of playing cards: you start with one card, then pick up the next card and place it in its correct position relative to the first card, then continue with the subsequent cards.
How Insertion Sort Works
The algorithm divides the input array into two parts:
- A sorted portion at the left end of the array
- An unsorted portion at the right end of the array
Key Steps of Insertion Sort
- Start with the first element, which is considered already sorted
- Take the next unsorted element
- Compare it with the elements in the sorted portion
- Shift larger elements to the right to make space
- Insert the element in its correct position
- Repeat until all elements are sorted
My own implementation
#include
int array[] = {67,34,12,21,35,5,2,1,0};
void insert_sort(int array[], int arraySize);
void stampa_array(int array[], int arraySize);
int main(void){
int arraySize = sizeof(array)/sizeof(array[0]);
printf("Array disordinato: ");
stampa_array(array, arraySize);
insert_sort(array, arraySize);
printf("Array ordinato: ");
stampa_array(array, arraySize);
return(0);
}
void stampa_array(int array[], int arraySize){
int i;
for(i = 0; i < arraySize; i++){
printf(" %d",array[i]);
}
printf("\n");
}
void insert_sort(int array[], int arraySize){
int j;
for(j = 1; j < arraySize; j++){ int key = array[j]; int i = j - 1; while(i >= 0 && array[i] > key){
array[i + 1] = array[i];
i = i - 1;
}
array[i + 1] = key;
}
}
C Implementation Breakdown
Function Signature
void insert_sort(int array[], int arraySize)Detailed Code Analysis
void insert_sort(int array[], int arraySize){
int j;
for(j = 1; j < arraySize; j++){ // Outer loop: traverse unsorted portion int key = array[j]; // Current element to be inserted int i = j - 1; // Last index of sorted portion // Inner loop: shift and find insertion point while(i >= 0 && array[i] > key){
array[i + 1] = array[i]; // Shift larger element right
i = i - 1; // Move backwards in sorted portion
}
array[i + 1] = key; // Insert element in correct position
}
}Loop Mechanics
- Outer Loop (j)
- Starts from second element (index 1)
- Processes each unsorted element in the array
- Inner Loop (while)
- Shifts elements greater than ‘key’ to the right
- Finds the correct insertion point for ‘key’
Complexity Analysis
Time Complexity
| Scenario | Time Complexity |
|---|---|
| Best Case (Already Sorted) | O(n) |
| Average Case | O(n²) |
| Worst Case (Reverse Sorted) | O(n²) |
Space Complexity
O(1) – In-place sorting algorithm, uses only a constant amount of extra memory.
Pros and Cons
Advantages
- Simple and easy to implement
- Efficient for small datasets
- Adaptive (performs better on partially sorted arrays)
- Stable sorting algorithm
- Minimal additional memory required
Disadvantages
- Inefficient for large datasets
- Quadratic time complexity
- Performance degrades quickly with increasing array size
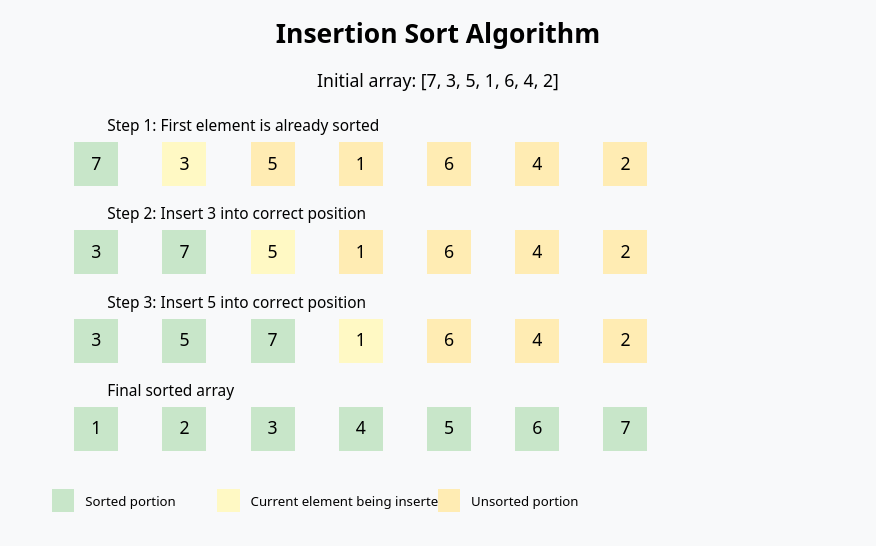
Example Walkthrough
Consider the array: [67, 34, 12, 21, 35, 5, 2, 1, 0]
- First iteration (j=1): [34, 67, 12, 21, 35, 5, 2, 1, 0]
- Second iteration (j=2): [12, 34, 67, 21, 35, 5, 2, 1, 0]
- Continues until fully sorted: [0, 1, 2, 5, 12, 21, 34, 35, 67]
When to Use Insertion Sort
- Small datasets (less than 50 elements)
- Nearly sorted arrays
- Online sorting (when data is received one element at a time)
Conclusion
While not suitable for large-scale sorting, Insertion Sort remains an important algorithm to understand. Its simplicity makes it an excellent learning tool for understanding sorting concepts.